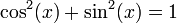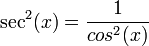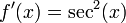Ejercicios Propuestos
1. Un ni~no usa una pajilla para beber agua de un vaso conico (con el vertice hacia abajo) a razon de 3 cm3/seg. Si la altura del vaso es de 10 cm y si el diametro de la parte superior es de 6 cm, >con que rapidez baja el nivel del agua cuando la profundidad es de 5 cm? >Cual es la variacion del radio en ese mismo instante?
2. La longitud del largo de un rectangulo disminuye a razon de 2 cm/seg, mientras que el ancho aumenta a razon de 2 cm/seg. Cuando el largo es de 12 cm y el ancho de 5 cm, hallar:
a. la variacion del area del rectangulo
b. la variacion del perimetro del rectangulo
c. la variacion de las longitudes de las diagonales del rectangulo
3. Dos lados de un triangulo miden 4 m y 5 m y el angulo entre ellos aumenta con una rapidez de 0,06 rad/seg. Calcule la rapidez con que el area y la altura del triangulo se incrementan cuando el angulo entre los lados es de ¼=3.
4. Una luz esta en el suelo a 45 metros de un edificio. Un hombre de 2 metros de estatura camina desde la luz hacia el edificio a razon constante de 2 metros por segundo. >A que velocidad esta disminuyendo su sombra sobre el edificio
en el instante en que el hombre esta a 25 metros del edi¯cio?
5. Un globo esta a 100 metros sobre el suelo y se eleva verticalmente a una razon constante de 4 m/seg. Un automovil pasa por debajo viajando por una carretera recta a razon constante de 60 m/seg. >Con que rapidez cambia la distancia entre el globo y el automovil 1=2 segundo despues?
Calculo
En este blog encontraras explicaciones y tips que te pueden servir en tu estudio.
martes, 13 de septiembre de 2011
lunes, 12 de septiembre de 2011
Razones Trigonometricas
La derivación de las funciones trigonométricas es el proceso matemático de encontrar el ritmo al cual una función trigonometrica cambia respecto de la variable independiente; es decir, la derivada de la función. Las funciones trigonométricas más habituales son las funciones sin(x), cos(x) y tan(x). Por ejemplo, al derivar f(x) = sen(x), se está calculando la función f'(x) tal que da el ritmo de cambio del sen(x) en cada punto x.
Derivada de la función seno
A partir de la definición de la derivada de una función f(x):
Por tanto si f(x) = sin(x)
A partir de la identidad trigonométrica sin(A + B) = (sin(A)cos(B) + cos(A)sin(B), se puede escribir
Agrupando los términos cos(x) y sin(x), la derivada pasa a ser
Reordenando los términos y el límite se obtiene
Ahora, como sin(x) y cos(x) no varían al variar h, se pueden sacar fuera del límite para obtener
El valor de los límites
Son 1 y 0 respectivamente por Teorema del sándwich. Por tanto, si f(x) = sin(x),
[editar] Derivada de la función coseno
Si f(x) = cos(x)
A partir de la identidad trigonométrica cos(A + B) = cos(A)cos(B) − sin(A)sin(B), se puede escribir
Operando se obtiene
Como sin(x) y cos(x) no varían al variar h, se pueden sacar fuera del límite para obtener
El valor de los límites
Son 1 y 0 respectivamente. Por tanto, si f(x) = cos(x),
[editar] Derivada de la función tangente
A partir de la regla del cociente, según la cual si la función que se quiere derivar,  , se puede escribir como
, se puede escribir como
 , se puede escribir como
, se puede escribir comoy 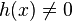 , entonces la regla dice que la derivada de
, entonces la regla dice que la derivada de  es igual a:
es igual a:
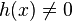 , entonces la regla dice que la derivada de
, entonces la regla dice que la derivada de  es igual a:
es igual a:A partir de la identidad trigonométrica
haciendo:
sustituyendo resulta
operando
y aplicando las identidades trigonométricas
resulta
BIBLIOGRAFIA: WIKIPEDIA
lunes, 15 de agosto de 2011
Reglas de derivacion
Reglas de derivaciónTeoremaDerivada de una constante por una funciónH) f es derivable en x=a ejercicioT) (kf(a))' = k.f'(a) f'(a)
------^------
k.f(x) - k.f(a) (f(x) - f(a))
(k.f(a))' = lim ---------------- = lim k ------------- = k.f'(a)
x->a x - a x->a x - a Nota:
TeoremaDerivada de la sumaLa derivada de una suma de funciones es la suma de las derivadas de cada función. Demostración: H) f es derivable en x=a, g es derivable en x=a T) f+g es derivable en x=a (f+g)'(a) = f'(a) + g'(a) (f+g)(x) - (f+g)(a) f(x) + g(x) - f(a) - g(a)
(f+g)'(a) = lim ------------------- = lim -------------------------
x->a (x-a) x->a (x-a)
f(x) - f(a) g(x) - g(a)
= lim ----------- + ------------ = f'(a) + g'(a)
x->a (x-a) (x-a)Notas:
Ejemplo(x + Lx)' = x' + (Lx)' = 1 + 1/xTeoremaDerivada del productoH) f es derivable en x=a, g es derivable en x=a Demostración: T) f.g es derivable en x=a (f.g)'(a) = f'(a).g(a) + f(a).g'(a) (f.g)(x) - (f.g)(a) f(x).g(x) - f(a).g(a)
(f.g)'(a) = lim ------------------- = lim --------------------
x->a (x-a) x->a (x-a)
f(x).g(x) - f(a)g(a) + f(a)g(x) - f(a)g(x)
= lim ------------------------------------------ =
x->a (x-a)
f'(a) g'(a)
(*) g(a) -----^----- -----^-----
-^- (f(x) - f(a)) (g(x) - g(a))
lim g(x)------------- + f(a)------------- = f'(a).g(a) + g'(a).f(a)
x->a (x-a) (x-a)(*) Pues g es derivable en a => (teorema) g es continua en a=> (def. de continuidad) existe g(a) y Notas:
Ejemplo(x2.sen x)' = 2xsen x + x2cos xTeoremaDerivada del cocienteH) f es derivable en x=a, g es derivable en x=a, g(a) distinto de 0 Demostración:T) f/g es derivable en x=a (f/g)'(a) = (f'(a).g(a) - f(a).g'(a))/g2(a) (f/g)(x) - (f/g)(a) f(x)/g(x) - f(a)/g(a)
(f/g)'(a) = lim ------------------- = lim ---------------------
x->a x - a x->a x - a
f(x)g(a) - g(x)f(a) + f(a)g(a) - f(a)g(a)
= lim ----------------------------------------- =
x->a (x - a)g(x)g(a)
f'(a) g'(a)
-----^----- -----^-----
(f(x) - f(a)) (g(x) - g(a))
g(a)------------- - f(a)------------- g(a)f'(a) - f(a)g'(a)
lim x - a x - a = --------------------
x->a ------------------------------------ g2(a)
g(x)g(a)
'--> g(a) (*) (*) Pues g es derivable en a => (teorema) g es continua en a=> (def. de continuidad) existe g(a) y Nota:
Ejemplo(cos x)x2 - (sen x)2x xcos x - 2sen x
(sen x/x2)' = --------------------- = ---------------
x4 x3TeoremaDerivada de la función compuestaRegla de la cadenaH) f es derivable en x=a, g es derivable en x=f(a) Demostración:T) gof es derivable en x=a (gof)'(a) = g'[f(a)].f'(a) g[f(x)] - g[f(a)]
(gof)'(a) = [g[f(x)]'(a) = lim ----------------- =
x->a x - a
g'[f(a)] f'(a)
--------^-------- ----^----
g[f(x)] - g[f(a)] f(x) - f(a)
lim ------------------ . ---------- = g'[f(a)].f'(a)
x->a f(x) - f(a) x - aNota:
Ejemplo 1h(x) = ex2 + 2xh es la composición de g(x) = ex y f(x)=x2 + 2x. h'(x) = g'[f(x)].f'(x) = ex2+2x.(2x + 2) Ejemplo 2h(x) = sen(x2)h es la composición de g(x)=sen x y f(x)=x2. h'(x) = g'[f(x)].f'(x) = cos (x2).2x TeoremaDerivada de la función inversaH) f es derivable en x=a (f'(a) distinto de 0) Demostración:f-1(x) es continua en f(a) T) f-1 es derivable en x=f(a). [f-1(f(a))]' = 1/f'(a) Queremos calcular f-1(x) - f-1(f(a)) f-1(x) - a lim ----------------- = lim ------------ x->f(a) x - f(a) x->f(a) x - f(a)Definamos g(x)=(f(x) - f(a))/(x - a) para todo x distinto de a. Consideremos (gof-1)(x) / (gof-1)(x) = g[f-1(x)] 1) lim f-1(x) = a pues f-1(x) es continua en f(a) por H)
x->f(a)
f(x) - f(a)
2) lim g(x) = lim ----------- = f'(a) pues f es derivable en a
x->a x->a x - a por H)=> De 1) y 2) por lim g[f-1(x)] = f'(a)
x->f(a)
f[f-1(x)] - f(a) x - f(a)
g[f-1(x)] = ---------------- = ----------
f-1(x) - a f-1(x) - a
f-1(x) - a 1
=> lim ------------ = -----
x->f(a) x - f(a) f'(a)
Nota:
Ejemplo
| ||||||
domingo, 24 de julio de 2011
Concepto de Derivada
Al hablar del concepto de Derivada es inevitable vincularlo con el concepto de limite.
Primero que todo tenemos que retomar cual es la ecuación de una recta en función de dos puntos conocidos (a,b) y (a',b') :
Como podemos ver el segundo término de la ecuación es a lo que llamamos la pendiente de la recta , y nos da la pendiente que tiene la recta respecto a la paralela al eje x.
Al tener una función f(x) y ambos puntos pertenecen a ella entonces estamos es calculando la ecuación de la recta secante (corta a la función en dos puntos) :
Por ende se afirma que:

Si a la hora de distanciar los dos puntos h se va haciendo cada vez más pequeña (h tiende a 0 ) obtendríamos una recta tangente (corta a la función en un solo punto)
La ecuación de la recta se da por:
Donde m es la pendiente y es igual a:
Finalmente a la pendiente o inclinacion de la linea recta tangente tiene como nombre derivada de la función en ese punto :
Si reemplazamos el punto x0 = 1 el resultado sera :
f '(1) = 2 · 1 = 2
Por ende la pendiente o inclinacion de la recta tangente es positiva y tiene un valor de 2 .
Que la inclinacion de la recta sea de signo positivo quiere decir que en ese punto la función es creciente , es decir , al aumentar la x aumenta la y .
¿En que podemos aplicar en concepto de derivada?
Si en el ejemplo anterior sustituimos el punto x0 = -1 obtendremos que
f '(-1) = 2 · (-1) = -2
En esta ocasion la pendiente es negativa contraria a la anterior por lo que la función en este punto es decreciente.
Al analizar todo el tema el valor de la derivada de esta función en un punto cualquiera , encontramos que si x0 es positivo , la derivada f '(x0) es positiva y por lo tanto la función es creciente y si el punto x0 es negativo la derivada f '(x0) es negativa y por lo tanto la función es decreciente .
¿Qué sucede en el punto x0 =0? Que no es crece ni decrece lo que pasa en este caso es que tenemos un mínimo ya que la función pasa de ser decreciente a la izquierda a creciente por la derecha.
En conclusión la aplicación de las derivadas es que nos puede servir para estudiar las diferentes funciones.fuente: http://www.terra.es/personal/ijic0000/deriv.htm
Ejercicios resueltos:
f(x) = 3x2 en x = 2.
f(x) = x2 + 4x − 5 en x = 1.




















 en x = 2.
en x = 2. en x = 3.
en x = 3. en x = 2.
en x = 2.




Calcular derivada de f(x) = x2 − x + 1 en x = −1, x = o y x = 1.

f'(−1), f'(0) y f'(1).
f'(−1) = 2(−1) − 1 = −3
f'(0) = 2(0) − 1 = −1
f'(1) = 2(1) − 1 = 1
Calcular derivada de  en x = −5.
en x = −5.
 en x = −5.
en x = −5.
Calcular derivada de  en x = 1.
en x = 1.
 en x = 1.
en x = 1.



Calcular derivada de  en x = 2.
en x = 2.
 en x = 2.
en x = 2.


Ejercicios de Tarea:
 en x = 2.
en x = 2. en x = 3.
en x = 3. Fuente: http://www.vitutor.com/fun/4/e_e.html
Suscribirse a:
Entradas (Atom)











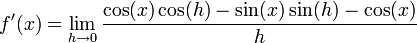





![\frac{d}{dx}f(x) = f'(x) = \frac{g'(x)h(x) - g(x)h'(x)}{[h(x)]^2}](http://upload.wikimedia.org/math/b/b/3/bb36df8c011f8e7202d7ae273feca2cd.png)

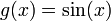

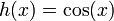
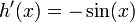
![f'(x) = \frac{\cos(x)\cos(x) - \sin(x)[-\sin(x)]}{\cos^2(x)}](http://upload.wikimedia.org/math/6/1/e/61eaf87c8478ac06854f652b444b239f.png)